Glossary

Bayesian inference

A method by which the probability of a given state is updated as more evidence becomes available.

Specifically, Bayesian inference calculates the posterior probability \(P(A\mid B)\) given a prior probability and a likelihood function, where \(P(A\mid B)\) is found using Bayes’ theorem.

Bayesian inference is a straightforward approach to state estimation, as in Monte Carlo Localization (MCL).

Bayes’ theorem

A core theorem in probability, including in decision theory, that describes the conditional relationship between two random variables.

\[P(A|B)=\frac{P(B|A)P(A)}{P(B)}=\frac{\mathtt{likelihood}\times \mathtt{prior}}{\mathtt{normalization}}\]

Given a linear transformation \(T\) and nonzero vector \(\bf{v}\), then \(\bf v\) is an eigenvector of \(T\) if \(T(\bf{v})=\lambda v\). We call the scalar factor \(\lambda\) the eigenvalue of \(\bf v\).

Here is an illustration from Wikipedia:

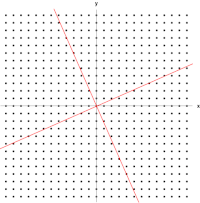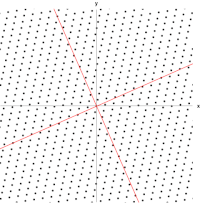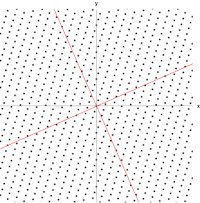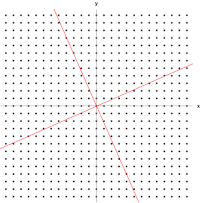
A 2×2 real and symmetric matrix representing a stretching and shearing of the plane. The eigenvectors of the matrix (red lines) are the two special directions such that every point on them will just slide on them. Jacopo Bertolotti, CC0, via Wikimedia Commons

Markov property

Within a stochastic (that is, a random) process, the process has the Markov property if the conditional probability distribution of its future states depend solely on the current state, not on the past. Markov processes can therefore have their future states estimated solely by considering their current state.

Monte carlo method

A broad class of algorithms that use a finite number of randomly sampled points to compute a result.

Multivariate normal (Gaussian) distribution

The multivariate normal distribution \(\mathcal{N}\) is a generalized of a simple 2D “bell curve” described by the mean vector \(\boldsymbol\mu\) and the covariance vector \(\boldsymbol\Sigma\).

arrow_back Back home